Pour l’étude du cas d’accident qui est précédemment présenté, nous allons normalement faire la reconstitution cinématique en établissant le scénario des évènements successifs pour chacun des véhicules impliqués depuis leurs situations de conduite initiale jusqu’a leurs positions finales respectives. rappel des faits accidentogènes: les faits : le 18.04.2005 à 18h15 sur le département 4… deux véhicules circulaient le véhicule symbolisé A :VP Ford Focus le véhicule symbolisé B : VP Seat Ibiza Le véhicule A conduit par son propriétaire DN circule sur une VC à l’intersection avec la D8.. au lieu dit C de L’H.., le VL A ne respecte pas la priorité au VL B imposé par le panneau cédez le passage. Il s’agit d’une intersection en T comme le montre le plan de l’accident. Le véhicule B traversait naturellement l’intersection pour pénétrer par le portail dans sa propriété. Le véhicule A venait de sa droite, la ligne pour lui était droite, à l’intersection il avait une balise de priorité et il allait en face. Il n’a pas vu la voiture B qu’il a percuté sur le flanc droit comme le montreront les photos.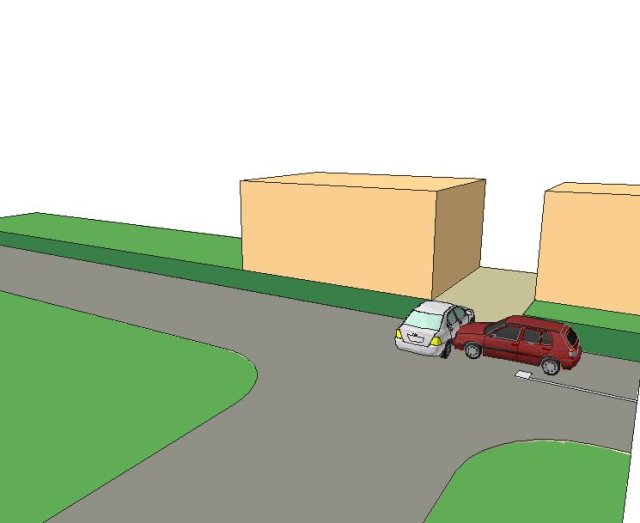 
Sur l’impact la voiture B a fait un demi tour complet pour percuter avec l’arrière gauche violemment le mur de clôture en pierre ensuite malgré le fossé profond la voiture est revenue sur la route en finissant son trois quart de tour. 
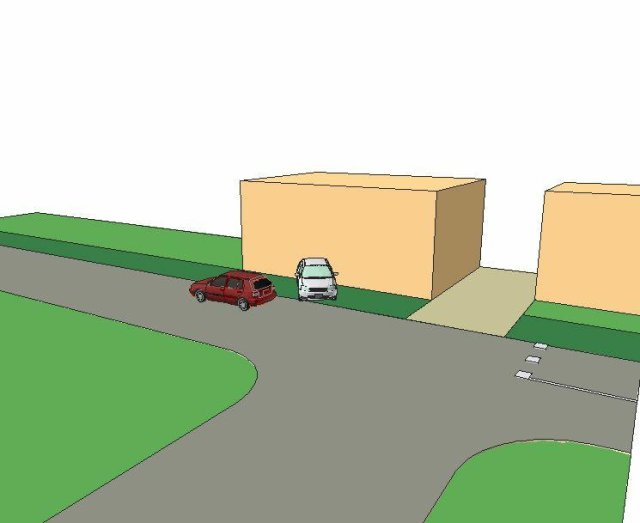La voiture A est passée devant et les gendarmes ont négligé la position d’après le choc pour celle ci, déclarant qu’elle avait été bougée avant leur arrivée. note: le père de l’accidentée B lui déclare que c’est faux car il est sorti au bruit de l’impact et il n’a plus bougé de l’endroit aussi affirme t il que les position d’après accident étaient comparables a celle du relevé par la gendarmerie. 
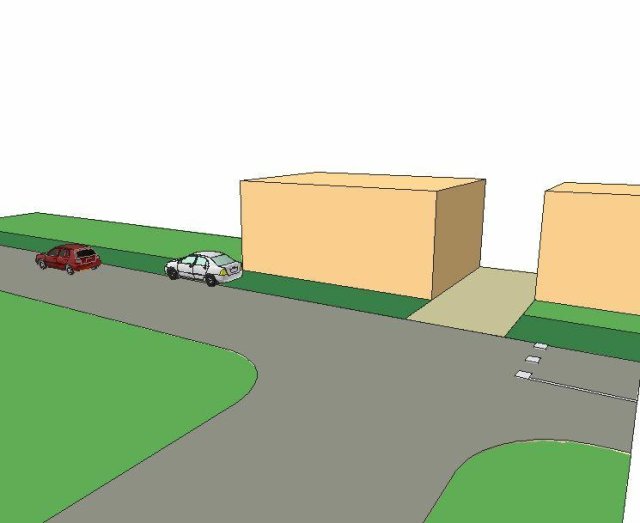– l’enquête préliminaire avec l’audition du conducteur du véhicule A ou il explique avoir 22 ans être mécanicien monteur et rentrer de son travail vers 18h00 sur un itinéraire habituel en étant seul a bord de son véhicule. Il précise qu’au niveau de l’intersection il n’a rien vu a sa gauche et il est rentré dans le carrefour pour y voir devant le flanc du véhicule B qu’il a percuté, le coussin d’air bags s’est développé. Il indique que sa voiture s’était arrêtée devant l’autre voiture et qu’il l’a poussé pour la dégager. Il indique ensuite qu’il était en quatriême et qu’il pense qu’il roulait entre 80 et 90 kmh enfin il déclare avoir son permis depuis le 09.12.2002. 
PRINCIPES DE CALCULS Au moment de la collision, les véhicules FORD Focus (A) et SEAT Ibiza (B) possédaient chacun une énergie cinétique Ec (A) et Ec (B) fonction de leur masse et de leur vitesse, selon la relation : Ec = ½ .M.V2 la somme de ces énergies a été dissipée au cours des différents évènements du sinistre. A chaque événement correspond une énergie absorbée, Les différents événements sont: freinage avant choc chocs avec déformations des véhicules ripages après les chocs Nous retiendrons que ; n’ayant pas vu arriver le véhicule A, le conducteur du véhicule B n’a pas freiné. Pour ce qui concerne le freinage du véhicule A, il n’y a pas de trace car équipé d’un système ABS, nous n’en tiendrons compte qu’une fois avoir estimé sa vitesse à l’instant du choc. Cet accident peut donc se décomposer en six phases: EA (def1) = déformation de A …. au choc avec B EB ( def1) = déformation de B ….au choc avec A EA (Rip1) = Ripage de A après le choc avec B EB (Rip1) = ripage de B après le choc avec A EB (def2) = déformation de B du au choc contre le mur l’énergie totale que possédait les deux véhicules juste avant le choc initial est égale à la somme des énergies dissipées soit: Ec(A) + Ec (B) = EA ( def1) + EB (def 1) + EA (rip1 + EB (Rip1) + EB (def2) + EB (Rip2) Poids et mesures des distances Poids véhicule A = 1200 kg + 80 kg = 1280 kg (80 kg = poids conducteur un homme) Poids véhicule B = 1175 + 65 kg = 1240 kg (65 kg = poids conducteur une femme) Distance choc initial et choc au mur par B 10.50 m Distance choc initial et immobilisation 19.00 m Distance choc mur pour B et immobilisation = 3.40 m Energie cinétiqe de B avant le choc La vitesse de B peut être estimée entre : 10 km/h = 2.78 m/s 5 km/h = 1.39 m/s Le véhicule B n’ayant pas freiné avant le choc son énergie dissipée est donc nulle. L’énergie de B avant le choc est donc fonction de sa vitesse et de sa masse selon la relation : Ec (B) = ½ x M (B) x V (B) 2 M (B) = 1240 V (B) = 2.78 a 1.39 m/s Ec (B) mini = 1240 x 1.39 2 = 1198 joules 2 Ec ( B ) maxi = 1240 x 2.78 2 = 4792 joules 2 Au moment du choc B avait une énergie cinétique comprise entre : 1198 et 4792 joules Energie cinétique dissipée lors du choc initial pour les déformations de A et de B Nous utiliserons pour cela la méthode du NTHSA Le NTHSA ( National Highway trafic safety administration US département of transportation accident investigation division national center on …… and analyses) a défini , après de nombreux essais, une formule expérimentale. Cette formule permet de calculer l’énergie absorbée par les déformations en fonction des caractéristiques du véhicule, de la largeur et de la profondeur des déformations ainsi que de la localisation et de l’angle de choc ( source : trafic accident reconstitution northwestern university trafic institute evanston Illinois) E= W/6.6 g + A (C1 + 2C 2 + 2 C 3 + C 4 ) + B/3 ( C1 2 + 2C 2 2 + 2 C 3 2 + C4 2 + C1) * ( C3 + C4) X 1 … tg2 E = énergie dissipée en pouces par livres W largeur de la déformation en pouces A;B;G sont des constantes fonction des caractéristiques (dimension et rigidité) du véhicule et de la localisation du choc (frontal, latéral, arrière) C = profondeur de chaque déformation occasionnée par le choc en pouces O/ = angle entre la perpendiculaire à la surface de contact et à la direction du choc en degré Energie dissipée par la déformation de A les déformations s’étendent sur toute la largeur du véhicule soit : W = 170 cm le recul du pare choc avant est de 50 cm sur toute la largeur l’angle de choc O/ = 0° C1 = C2 = C3 = C4 = C5 = 50 cm = 19.7 in les coefficients de raideurs d’une SEAT IBIZA SDI est selon la source « traffic accident reconstitution » pour un avant : A = 259 ib/in ; B = 43 ib/in; G = 778 ib/in En appliquant ces valeurs à l’équation présentée ci dessous nous obtenons: Donnée valeur unité valeur unité commentaire W 66.93 in 170.00 cm largeur de la déformation A 259.00 lb/in kg/m force max / pouce causant une Déformation permanente B 43.00 lb/in² kg/m² Rigidité par pouces de déformation G 778.00 lb kg G A²/2b ¤ 0.00° angle : normale à la surface de Contact/la direction du choc C1 19.69 in 50.00 cm déformation relevée 1 C2 19.69 in 50.00 cm déformation relevée 2 C3 19.69 in 50.00 cm déformation relevée 3 C4 19.69 in 50.00 cm déformation relevée 4 C5 19.69 in 50.00 cm déformation relevée 5 E 950 909 in.lbs 107 475 j Energie dissipée par la déformation de B la déformation s’étend sur la longueur droit du véhicule soit W = 200 cm l’angle de choc est O/ = 0° 1° CAS 2° CAS C1 = 10cm C1 = 35 cm C2 = 20 C2 = 35 C3 = 35 C3 = 35 C4 = 20 C4 = 35 C5 = 10 C5 = 35 les coefficients de raideur d’une FORD FOCUS pour un choc latéral est: A=173 Ib/cm ; B = 57 Ib/cm ; G = 263 Ib/cm En appliquant ces valeurs à l’ équation présentées ci dessus nous obtenons: Donnée valeur unité valeur unité commentaire W 78.74 in 200.00 cm largeur de la déformation A 173.00 lb/in kg/m force max / pouce causant une Déformation permanente B 57.00 lb/in² kg/m² Rigidité par pouces de déformation G 263.00 lb kg G A²/2b ¤ 0.00° angle : normale à la surface de Contact/la direction du choc C1 3.94 in 10.00 cm déformation relevée 1 C2 7.87 in 20.00 cm déformation relevée 2 C3 13.78 in 35.00 cm déformation relevée 3 C4 7.87 in 20.00 cm déformation relevée 4 C5 in 10.00 cm déformation relevée 5 E 352 614 in.lbs 39 854 j Donnée valeur unité valeur unité commentaire W 78.74 in 200.00 cm largeur de la déformation A 173.00 lb/in kg/m force max / pouce causant une Déformation permanente B 57.00 lb/in² kg/m² Rigidité par pouces de déformation G 263.00 lb kg G A²/2b ¤ 0.00° angle : normale à la surface de Contact/la direction du choc C1 13.78 in 35.00 cm déformation relevée 1 C2 13.78 in 35.00 cm déformation relevée 2 C3 13.78 in 35.00 cm déformation relevée 3 C4 13.78 in 35.00 cm déformation relevée 4 C5 13.78 in 35.00 cm déformation relevée 5 E 634 512 in.lbs 71 715 j Energie dissipée par la déformation de B contre le mur la déformation s’étend sur l’ angle arrière gauche du véhicule soit W= 100 cm l’angle du choc est de O/ = 45° 1° CAS 2° CAS C1 = 10 cm C1 = 20 cm C2 = 20 cm C2 = 40 cm C3 = 10 cm C3 = 20 cm les coefficients de raideurs d’une FORD FOCUS avec un choc arrière est de : A = 410 Ib/cm; B = 44 Ib/cm ; G = 1931 Ib/cm Nous considérons que le mur n’a pas absorbé d’ énergie Donnée valeur unité valeur unité commentaire W 39.37 in 170.00 cm largeur de la déformation A 173.00 lb/in kg/m force max / pouce causant une Déformation permanente B 57.00 lb/in² kg/m² Rigidité par pouces de déformation G 263.00 lb kg G A²/2b ¤ 45° 45 angle : normale à la surface de Contact/la direction du choc C1 7.87 in 20.00 cm déformation relevée 1 C2 15.75 in 40.00 cm déformation relevée 2 C3 7.87 in 20.00 cm déformation relevée 3 E 141 250 145 965 j Donnée valeur unité valeur unité commentaire W 39.37 in 170.00 cm largeur de la déformation A 173.00 lb/in kg/m force max / pouce causant une Déformation permanente B 57.00 lb/in² kg/m² Rigidité par pouces de déformation G 263.00 lb kg G A²/2b ¤ 45° 45 angle : normale à la surface de Contact/la direction du choc C1 7.87 in 20.00 cm déformation relevée 1 C2 15.75 in 40.00 cm déformation relevée 2 C3 7.87 in 20.00 cm déformation relevée 3 E 377 736 in.lbs 42 693 j Energie dissipée par B lors des ripages avant le choc contre le mur Distance ripage = 10.50 mètres le véhicule B a opéré un mouvement de rotation d’ amplitude 180° soit un demi tête à queue (180° = TT radiant) Sur les 10.5 mètres de ripage se sont effectués par moitié sur le bitume sec et par moitié sur l’herbe coefficient d’ adhérence: Bitume sec = 0.55 herbe sèche = 0.31 Donc le coefficient retenu sera 0.55 + 0.31 = 0.43 2 L’expression de l’ énergie dissipée est de forme E (B) vip1 = M (B) x g x F x d x TT M ( B) = 1240 kg g = 9.81 m/s2 E = 0.43 d = 10.5 m m = 3.1416 E (B) rip 1 = 1240 x 9.81 x 0.43 x 10.5 x 3.1416 E (B) rip 1 172544 joules Energie dissipée par B lors du ripage après le choc contre le mur Distance du ripage : 3,40 mètres Le véhicule B a opéré un mouvement de rotation d’amplitude soit un tête à queue de )90° = TT radian ) Sur les 3,40 m de ripage ils se sont effectués moitié sur herbe et moitié sur bitume avec un coefficient d’ adhérence de 0.43 comme démontré plus haut L’expression de l’énergie dissipée est de : la forme: E (B) rip 2 = M (B) x 9 x F x d x TT 2 MB = 1240 kg 9 = 9.81 m/s2 F = 0.43 d = 3,40 m TT = 3,1416 = 1, 57 2 2 E ( B ) rip 2 = 1240 x 9.81 x 0.43 x 3,40 x 1,57 E (B) rip 2 = 27921 joules Energie dissipée par A lors du roulage après le choc initial distance du roulage : 19 m le coefficient de résistance au roulement sur du macadam ou goudron sec d’après les études dynamiques des véhicules à moteur réalisés par BOSCH soit 0.025 l’expression de l’énergie dissipée est de la forme : E ( A) rlt = M (A) x 9 x F x d A ( A ) = 1280 kg g = 9.81 m/s F = 0.025 d = 19 m E (A) rlt = 1280 x 9.81 x 0.025 x 19 E ( A) rlt = 5964 joules RESULTAT DE L’ ETUDE l’énergie totale que possédait les deux véhicules juste avant le choc est égale à la somme des énergies dissipées soit Ec (A) = E (A) def + Ec ( B) def 1 + E ( B) rip 1 + E (B) rip 2 + E ( A) rlt – Ec (B) Ec (A) = 107475 + 39854 + 15965 + 172544 + 27921 + 5964 – 1198 = 368525 joules mini Ec ( A) = 107475 + 71715 + 42693 + 172544 + 27921 + 5964 – 4792 = 423560 joules maxi Au moment du choc le véhicule A possédait une énergie cinétique comprise entre 368525 et 423560 joules Vitesse du véhicule A au moment du choc l’énergie cinétique du véhicule B est fonction de sa vitesse et sa masse selon la relation Ec ( A) = 1 / 2 M (A) x V (A) 2 Connaissant l’énergie cinétique et la masse, on peut en déduire la vitesse de ( A ) suivant la relation: V (A) = v 2 x Ec (A) M (A) M (A) = 1280 kg Ec (A) mini = 368525 joules Ec (A) maxi = 423560 joules V (A) mini = v2 x 368525 = 23, 99 m/s = 86 km/h 1280 V (B) maxi = v2 x 423560 = 25,73 m/s = 93 km / h 1280 CONCLUSION Au moment du choc entre A et B la vitesse de A était comprise entre 86 et 93 kilomètres par heures. Ce résultat est obtenu en fonction des informations recueillie sur les lieux du sinistre , le plan du rapport de gendarmerie et les déformations constatées sur les véhicules A et B En sachant que a 90 km/h la distance d’arrêt d’un véhicule terrestre à moteur est de 70 mètres en tenant compte du temps de réflexe du conducteur, du délai de mise en œuvre des freins, de l’efficacité des freins bien réglés et de la décélération sur un sol horizontal et sec, en arrivant à cette vitesse, le conducteur de A ne pouvait s’arrêter que et seulement si il avait vu le véhicule B 70 mètres avant l’intersection.
Commentaires récents